1.1 개론
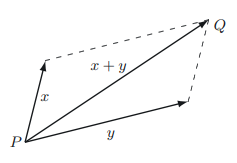
평행사변형 법칙(parallelogram low)
힘, 속도, 가속도 등 많은 물리 개념은 크기 뿐 아니라 방향 정보를 가지고 있다. 이처럼 크기와 방향을 모두 가진 물리량을 벡터(vector)라고 한다. 두 물리량이 함께 작용할 때, 크기뿐만 아니라 방향까지 고려해야한다. 두 벡터를 결합시키는 방법은 아래의 그림과 같으며 이를 평행사변형 법칙이라 한다.
스칼라 곱(scalar multiplication)
또한 벡터의 크기를 확대하거나 축소할 수 있는데, 이를 벡터에 실수를 곱하는 스카라 곱이라고 하고 그림으로 나타내면 아래와 같다. t > 0 일때 x 방향과 같고, t < 0 일 때 x 방향과 반대 방향이다.
벡터의 합과 스칼라 곱의 성질
1. x + y = y + x
2. (x + y) + z = x + (y + z)
3. x + O = x 를 만족하는 벡터 O가 존재
4. x + y = O 를 만족하는 벡터 y가 존재
5. 모든 실수 a, b 에 대해 벡터 x 는 (ab)x = a(bx)
6. a(x + y) = ax + ay
7. (a + b)x = ax + bx
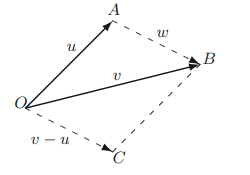
직선의 방정식
두점을 지나는 직선의 방정식은 적절한 실수 t에 대해 다음과 같이 표현될 수 있다.
$$ x = u + tw = u + t(v - u) $$
평면의 방정식
한 직선 위에 있지 않은 세점 A, B, C를 생각하자. 그럼 3개의 벡터를 통해 3점이 속한 평면위의 임의의 점을 표현할 수 있고 평면의 방정식을 구할 수 있다. 시작점을 A라고 했을 때 평면의 방정식은 아래와 같다.
$$ x = A +su + tv $$

1.2 벡터공간
체(field) 에서의 벡터공간(vector space) 또는 선형공간(linear space) V는 조건을(조건은 위의 벡터의 합과 스칼라 곱의 성질과 거의 같으므로 따로 적지 않겠다.) 만족하는 두 연산, 합과 스칼라 곱을 가지는 집합이다. (참고로 체의 가장 대표적인 예는 실수의 집합과 복소수 집합이다.)
- 합(sum)은 V의 두 원소 x, y에 대하여 유일한 원소 x + y ∈ V를 대응하는 연산이다.
- 스칼라 곱(scalar multiplication)은 field F의 원소 a와 벡터공간 V의 원소 x마다 유일한 원소 ax ∈ V를 대응하는 연산이다.
field F의 원소는 스칼라(scalar), 벡터공간 V의 원소는 벡터(vector)라 한다.
entry(component)
a1, a2, ..., an 가 field F의 원소일 때, \((a_1, a_2, ..., a_n)\) 꼴을 n순서쌍(n-tuple)이라한다. 그리고 순서쌍을 구성하는 성분을 entry 또는 component 라고 한다.
column vector
field F에서 가져온 모든 n순서쌍의 집합을 \( F^n \)이라 표기한다. u = \((a_1, a_2, ..., a_n)\) ∈ \(F^n\), v = \((b_1, b_2, ..., b_n)\) ∈ \(F^n\), c ∈ F일때, 이 집합은 F-벡터공간이다.
\(F^n\)의 벡터는 행벡터(row vector)보다는 열벡터(column vector)로 주로 표현한다.
\( \begin{pmatrix} a_1 & a_2 & ... & a_n \end{pmatrix} \) \( \begin{pmatrix} a_1 \\ a_2 \\ . \\ . \\ . \\ a_n \end{pmatrix} \)
matrix
filed F에서 성분을 가져온 m x n 행렬은 다음과 같이 직사각형 모양의 배열이다.
$$ \begin{pmatrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ . & . & . & . \\ a_{m1} & a_{m2} & ... & a_{mn} \end{pmatrix} $$
diagonal entry
위의 matrix에서 i=j인 \( a_{ij} \)를 이 행렬의 대각성분이라고 한다.
1.3 Subspace(부분공간)
정의
F-벡터공간 V의 부분집합을 W라고 생각하자. 이 부분집합 W가 V에서 정의한 합과 스칼라곱을 가진 F-벡터공간일 때, V의 부분공간 이라고 한다.
모든 벡터공간 V에 대하여 V와 {0}은 부분공간이다.
성질
1. 모든 x ∈ W, y ∈ W 에 대하여 x + y ∈ W이다. (W는 덧셈에 대하여 닫혀있다.)
2. 모든 c ∈ F와 모든 x ∈ W에 대하여 cx ∈ W이다. (W는 스칼라 곱에 대하여 닫혀있다.)
3. W는 영벡터를 포함한다.
전치행렬
\( A^t\) 는 A 행렬의 행과 열을 바꾼 행렬이다. 즉, \((A^t)_{ij} = A_{ji}\)
$$ \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}^t = \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix} $$
만약 \( A^t = A\)이면 대칭행렬이라고 한다.
upper triangular matrix
대각 성분아래의 모든 성분이 0인 행렬
$$ \begin{pmatrix} 1 & 4 & 3 & 5 \\ 0 & 5 & 6 & 8 \\ 0 & 0 & 3 & 6 \end{pmatrix} $$
그중에서 대각성분을 제외한 모든 성분이 0인 정사각 행렬을 diagonal matrix 라고 한다.
$$ \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 5 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 6 \end{pmatrix} $$
1.4 Linear Combination and Systems of Linear Equation
정의
V는 벡터공간이고, S는V의 공집합이 아닌 부분집합이라하면 유한개의 벡터 \(u_1, u_2 ..., u_n\) ∈ S 와 스칼라 \(a_1, a_2 ..., a_n\) 에 대하여 다음을 만족하는 벡터 v ∈ V 는 S의 일차결합(linear combination)이라고 한다.
$$ v =\ a_1v_1\ +\ a_2v_ 2\ +\ ...\ +\ a_nv_n $$
이때 v는 벡터 \(u_1, u_2 ..., u_n\) 의 일차결합이고 \(a_1, a_2 ..., a_n\) 은 이 일차결합의 계수(coefficient)이다.
출처 : Stephen H. Friedberg, Arnold J. Insel, Lawrence E. Spense - Linear Algebra (5th Edition)
